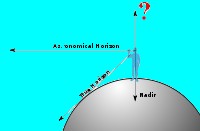
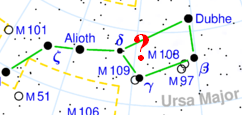
ASTRONOMIE (begrippen)
***************************************************************************************
Een supernova: klik hier.
Een hypernova: klik hier.
***************************************************************************************
*********************
Basisgeometrie
*********************
Dit is een kort overzicht van de geometrische concepten en formules die men nodig heeft voor een inleidende cursus sterrenkunde.
Hoeken
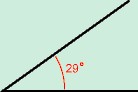 Hoeken kunnen worden gemeten in verschillende eenheden. Meestal uit men ze in graden. Net zoals een uur kan worden onderverdeeld in 60 minuten en een minuut van de tijd kan worden verdeeld in 60 seconden, kan een graad worden verdeeld in 60 boogminuten en een boogminuut kan verdeeld worden in 60 boogseconden.
Hoeken kunnen worden gemeten in verschillende eenheden. Meestal uit men ze in graden. Net zoals een uur kan worden onderverdeeld in 60 minuten en een minuut van de tijd kan worden verdeeld in 60 seconden, kan een graad worden verdeeld in 60 boogminuten en een boogminuut kan verdeeld worden in 60 boogseconden.
1 ° = 1 graad = 60' = 60 boogminuten
1' = 60" = 60 boogseconden
1 ° = 3600"
Extra uitleg over het begrip decimale graad. Klik hier.
Extra uitleg over het begrip ruimtehoek. Klik hier.
Werken met radialen: 2 pi radialen = 360 ° en 1 radiaal = 57,3 °.
Extra uitleg over het begrip radiaal. Klik hier.
Extra uitleg over het begrip sterradiaal. Klik hier.
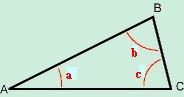
Hoeken kan men op verschillende manieren benoemen. Bijvoorbeeld, in deze driehoek
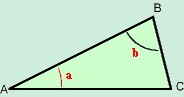 De hoek a kan ook worden opgeroepen BAC, en de hoek b kan ook worden opgeroepen ABC.
De hoek a kan ook worden opgeroepen BAC, en de hoek b kan ook worden opgeroepen ABC.
 Er zijn 90 ° in een rechte hoek.
Er zijn 90 ° in een rechte hoek.
De 3 hoeken van een driehoek zijn samen 180° groot: a + b + c = 180 °.
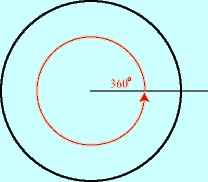
Er zijn 360 ° in een cirkel.
Hoeken en lijnen
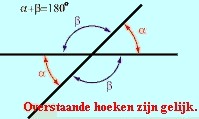 Wanneer twee lijnen elkaar snijden worden 4 hoeken gecreëerd. Elke twee overstaande hoeken zijn gelijk en de twee hoeken die naast elkaar liggen bedragen samen 180 °.
Wanneer twee lijnen elkaar snijden worden 4 hoeken gecreëerd. Elke twee overstaande hoeken zijn gelijk en de twee hoeken die naast elkaar liggen bedragen samen 180 °.
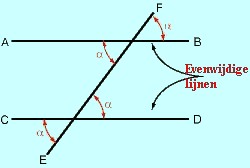 Wanneer twee lijnen evenwijdig zijn (zoals AB en CD), en gesneden worden door een lijn (EF) dan zijn de overliggende hoeken gelijk. ook de verwisselende binnehoeken en verwisselende buitenhoeken zijn 2 aan 2 gelijk. In combinatie met de bovenstaande regel, ziet men dat alle 4 de hoeken, gemarkeerd in het rood, gelijk zijn.
Wanneer twee lijnen evenwijdig zijn (zoals AB en CD), en gesneden worden door een lijn (EF) dan zijn de overliggende hoeken gelijk. ook de verwisselende binnehoeken en verwisselende buitenhoeken zijn 2 aan 2 gelijk. In combinatie met de bovenstaande regel, ziet men dat alle 4 de hoeken, gemarkeerd in het rood, gelijk zijn.
Cirkels
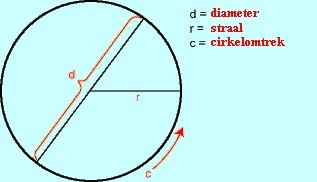
 d = 2 r (diameter = 2 maal de straal)
d = 2 r (diameter = 2 maal de straal)
c = pi d = 2 p r (de omtrek = pi maal de diameter of pi maal 2 keer de straal).
oppervlakte is pi r2 (de oppervlakte = straal maal straal maal pi) (pi = 3,14159 ... ).
De kleine hoek formule
Omtrek cirkel (c) = 2 pi r. De afstand van een deel van de cirkelomtrek berekenen. Bv. van de boog gemarkeerd door de letter s.
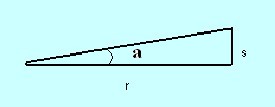
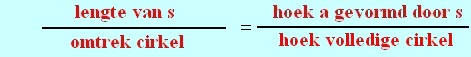
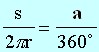
Waarom is deze formule zo goed? Omdat ze kan gebruikt worden voor dingen die geen deel uitmaken van een cirkel, zolang de hoek klein is! Bijvoorbeeld, wanneer de hoek klein is (minder dan 25), de driehoek hieronder heeft een zeer kleine scherpe hoek a en s is uiterst klein. Voor deze driehoek, is het een goede benadering om te zeggen dat s, r, gerelateerd zijn aan de kleine hoek formule. Nu heeft men inderdaad een zeer krachtig instrument , omdat men veel van de astronomie problemen kan omzetten in foto's met zeer kleine driehoeken.
Hoekmaten
In de sterrenkunde bestudeert men het heelal vanop de aarde. Dit betekent dat men de grootte van objecten niet kan meten met behulp van een liniaal. Dus vanuit de aardse observatie, berekent men vaak de grootte van een object met behulp van een te meten hoek. Als men geluk heeft iets over de afstand van een object te weten, dan kan men met behulp van de kleine hoek formule een relatie leggen tussen de hoekgrootte en de lineaire maat . Dit is een zeer frequente manier van meten van objecten in de astronomie.
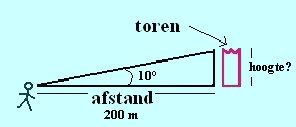
Stel dat men de hoogte van een toren die men van op een afstand van 200 m bekijkt moet bepalen. Men kijkt naar de hoogte van de toren onder een hoek van 10°. Zie onderstaande tekening en berekening.
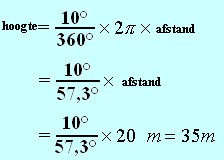
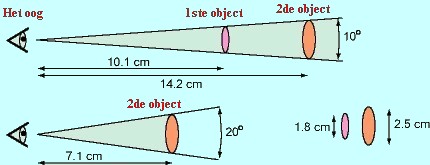 De bovenste tekening toont aan dat twee objecten met verschillende grootte dezelfde hoekgrootte kunnen hebben indien zij worden bekeken vanaf verschillende afstanden. De hoekgrootte van het object wordt bepaald door de verhouding grootte / afstand. De lineaire grootte van het 2de object (2,5 cm) is 1,4 keer zo groot als het 1ste object (1,8 cm) en moet zodanig worden geplaatst dat het 1,4 keer verder staat om het onder dezelfde hoek te zien. Verplaatst men het 2de object twee maal dichter (zie onderste tekening) dan wordt de hoekgrootte tweemaal zo groot (20 graden ipv 10 graden).
De bovenste tekening toont aan dat twee objecten met verschillende grootte dezelfde hoekgrootte kunnen hebben indien zij worden bekeken vanaf verschillende afstanden. De hoekgrootte van het object wordt bepaald door de verhouding grootte / afstand. De lineaire grootte van het 2de object (2,5 cm) is 1,4 keer zo groot als het 1ste object (1,8 cm) en moet zodanig worden geplaatst dat het 1,4 keer verder staat om het onder dezelfde hoek te zien. Verplaatst men het 2de object twee maal dichter (zie onderste tekening) dan wordt de hoekgrootte tweemaal zo groot (20 graden ipv 10 graden).
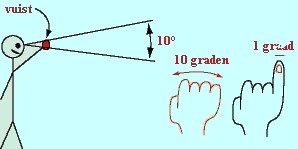 In de praktijk kan men de hoekgrootte van voorwerpen (bomen, sterrenbeelden, vrienden) meten met behulp van diverse lichaamsdelen. In nevenstaande figuur is de hoekgrootte van de vuist bij getrekte arm ongeveer 10 graden en de pink ongeveer 1 graad.
In de praktijk kan men de hoekgrootte van voorwerpen (bomen, sterrenbeelden, vrienden) meten met behulp van diverse lichaamsdelen. In nevenstaande figuur is de hoekgrootte van de vuist bij getrekte arm ongeveer 10 graden en de pink ongeveer 1 graad.
Samenvatting

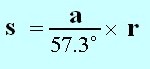
Merk op dat men de hoek in graden moet uitdrukken om de berekenigen naar behoren te verwerken. In de sterrenkunde werkt men met zeer kleine hoeken, gemeten in boogseconden. Men kan de graden veranderen in boogseconden met behulp van de conversie methoden.
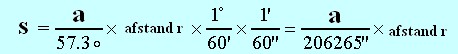
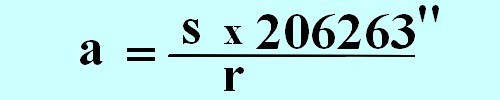
Voorbeeld van berekening:
Sommige objecten in de lucht hebben een schijnbare grootte - net als de maan. Door inzicht in de geometrie en de aard van een cirkel, is het mogelijk om de afstand te bepalen naar het object, of de fysieke diameter van het object. De standaard in de astronomie is de graad en de boogseconde. Hier zijn de conversie factoren:

Voor de bepaling van de fysieke diameter van Jupiter (op 26 juli 2003), kan men gebruik maken van de kleine hoek formule:
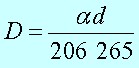 D = lineaire (fysieke) diameter.
D = lineaire (fysieke) diameter.
α = hoekgrootte in boogseconden = bekend voor Jupiter 31,2 boogseconden.
d = de afstand tot object = bekend voor Jupiter = 943.000.000 km
206265 = boogseconden per radiaal.
 Dit is in goede overeenstemming met de werkelijke diameter van Jupiter (142.984 km).
Dit is in goede overeenstemming met de werkelijke diameter van Jupiter (142.984 km).
************************************************************
Zonsopgang, zonsondergang en schemering
************************************************************
Zonsopgang, zonsondergang en schemering (voor Ukkel). Klik hier.
De tijdstippen van zonsopgang en zonsondergang zijn verschillend van dag tot dag en van plaats tot plaats.
Voor de berekening houdt men rekening met de straalbreking of refractie door de atmosfeer. Door de afbuiging van het licht kan men lichtstralen die hun oorsprong op 34 boogminuten (') onder de horizon hebben, al op de horizon waarnemen. Als het middelpunt van de zonneschijf, die zelf een diameter van ongeveer 32' heeft, nog 50' onder de horizon staat, ziet men de bovenrand al aan de horizon.
Als gevolg daarvan, duurt de dag rond 21 maart en rond 23 september, het begin van resp. lente en herfst, niet juist 12 uur, maar iets langer: 12 uur en 15 minuten. De duur van de schemering is 's avonds het tijdsinterval tussen zonsondergang en het ogenblik waarop de zon een aantal graden onder de horizon staat. 's Morgens is de schemering het interval tussen het ogenblik waarop de zon een aantal graden onder de horizon staat en de zonsopkomst.
Voor de zoncalculator. Klik hier.
Meestal verwijst men met schemering naar de burgerlijke schemering. In dat geval moet het middelpunt van de zonneschijf 6° onder de horizon staat. Voor de zogenaamde nautische schemering is dat 12°. Voor de astronomische schemering is 18° vereist, maar soms wordt hiervoor ook 15° gebruikt, omdat reeds dan zo goed als volledige duisternis is ingetreden. Vanaf eind mei tot begin oktober geraakt de zon in België niet tot op 18° onder de horizon. Dan komt er geen einde aan de astronomische schemering zodat we niet van een 'echte' astronomische nacht kunnen spreken. Op het einde van de burgerlijke schemering ('s avonds) of in het begin van de burgerlijke schemering ('s morgens) is het nog niet echt donker. Men zegt dat zolang de burgerlijke schemering duurt, het nog steeds mogelijk blijft om bij heldere hemel en in open lucht met de rug gericht naar het punt van zonsopkomst ('s morgens) of zonsondergang ('s avonds) een gewoon gedrukte tekst te lezen. Het spreekt vanzelf dat de plaatselijke meteorologische omstandigheden en de eventuele aanwezigheid van maanlicht de zichtbaarheid beïnvloeden.
Voor meer uitleg over tijdzone. Klik hier.
Voor meer uitleg over zomeruur. Klik hier.
Voor meer uitleg over tijdsvereffening. Klik hier.
********************************************************************************
Culmineren van een hemellichaam op het noordelijk halfrond
********************************************************************************
Een hemellichaam culmineert als het op de plaatselijke meridiaan staat. De plaatselijke meridiaan is een denkbeeldige lijn. Die loopt van het zuiden recht over het hoofd naar het noorden. Anders gezegd: het is de lijn, die de zuidpool, het zenit en de noordpool met elkaar verbindt. Staat een hemellichaam op de plaatselijke meridiaan, dan staat het dus altijd precies in het zuiden óf precies in het noorden. Denk eens aan de dagelijkse beweging van de zon. De zon komt op in het oosten. Ongeveer midden op de dag staat de zon in het zuiden. Hij culmineert als hij op de plaatselijke meridiaan staat. Tijdens deze culminatie staat de zon zo hoog mogelijk aan de hemel. Na de culminatie wordt de hoogte weer minder. De zon gaat in het westen onder. Rond middernacht staat hij precies in het noorden. De zon culmineert nu dus opnieuw. Nu bereikt hij juist zijn laagste stand. Hij staat zo ver mogelijk onder de horizon. Ieder hemellichaam culmineert zo twee maal per dag. De ene keer bereikt het hemellichaam de hoogste stand. De andere keer de laagste stand. Vaak is maar één van die twee culminaties zichtbaar. Net als bij de zon. Die culminatie vindt plaats in het zuiden als het hemellichaam de hoogste stand bereikt. Het kan ook zijn, dat men een ster twee maal per dag kan zien culmineren. Ook in zijn laagste stand staat zo'n ster nog boven de horizon. Precies in het noorden. Het zijn sterren, die nooit onder de horizon verdwijnen. We noemen ze circumpolaire sterren. De sterren van de Grote Beer zijn er een voorbeeld van. Staan de sterren in hun hoogste stand, dan spreekt men van bovenste culminatie. Staan ze in de laagste stand, dan heeft men het over onderste culminatie. Bij sommige sterren gebeuren beide culminaties in het noorden. Deze sterren staan vrij dicht bij de noordelijke hemelpool. Om precies te zijn: op minder dan 38 graden. Tenslotte zijn er ook sterren, die men op het noordelijk halfrond nooit kan zien culmineren. Dat zijn sterren, die nooit boven de horizon komen. Zelfs niet wanneer ze hun hoogste stand bereiken. Om ze te zien zou men ver naar het zuiden moeten reizen.
Hóe hoog een ster boven de zuidelijke horizon kan komen te staan is niet zo moeilijk zelf uit te rekenen. Men moet dan wel de declinatie van de ster weten. En ook de geografische breedte van de plaats waar men staat. Voor Utrecht is de geografische breedte ongeveer 52°. Voor Groningen is dat ongeveer 53° en voor Maastricht 51°. Men gebruikt de formule: culminatiehoogte = declinatie + 90 graden - geografische breedte. Een voorbeeld: De geografische breedte bedraagt 52°. De ster Aldebaran heeft een declinatie van +16°. De formule was: culminatiehoogte = declinatie + 90° - geografische breedte. Voor Aldebaran: culminatiehoogte = +16° + 90° - 52° = 54°. Hoger dan 54° boven de horizon kan Aldebaran in Utrecht nooit komen te staan.
Zonsopkomst en zonsondergang. Klik hier
Geografische coördinaten opzoeken. Klik hier.
Uitleg over de werking van de simulator van de zichtbaarheid van de zon en de sterren
Rechts boven: (achter days of year) tik je de datum in en kies je de maand of je verplaatst met de computermuis de rode pijl.
Observer's Latitude = breetegraad van de observeerder. Twee plaatsen met hun breedtegraad zijn reeds gegeven (Lincoln in Nebraska en Caïro in Egypte) Andere plaatsen kun je zelf kiezen. Achter latitude (breedte) tik je de gewenste breedtgraad in en kies je °N (noorderbreedte) of °S (zuiderbreedte) of je verplaatst met de computermuis de horizontale rode lijn op de wereldkaart.
Star Position = positie van de ster. Twee sterren met hun hemelcoördinaten zijn reeds gegeven (Sirius en Vega). Andere sterren kun je zelf kiezen door achter declination (declinatie) het gewenste getal in te tikken. Achter right ascension (rechte klimming) tik je ook het gewenste getal in. Zo heb je de hemelcoördinaten van de ster.
Onder aan (Daylight Hours and Star Visibility Timeline) is er een tijdlijn van 24 uur. De tijd gaat van (midnight) middernacht tot de volgende (midnight) middernacht. De grijze band duidt de nacht aan en de gele band het daglicht. Noon = middag (12 uur) De uren 3am, 6am, 9am, 3pm, 6pm, 9pm zijn ook aangegeven.
Klik je het keuzebolletje ("don't lock = niet vergrendelen) dan kun je met de computermuis de rode pijl over de tijdlijn bewegen. Over de wereldbol zie je dan de zon en de ster bewegen. Je kan ook de (sunrise) zonsopgang, de (noon) middagzon en de (sunset) zonsondergang aanklikken. Tenslotte kun je ook de (star rise) opkomst van de ster en de (star set) ondergang van de ster aanklikken. Een zwarte pijl duidt opkomst en ondergang van de ster aan op de tijdlijn. De blauwe lijn boven de tijdlijn geeft de tijd weer dat de ster (star above horizon) zichtbaar is boven de horizon. ook het (the start of twilight) beging van de schemering en het (the end of twilight) einde van de schemering kan men aanklikken.
Lijst van sterren met gegevens over o.a. de declinatie en rechte klimming. Klik hier.
****************************************************************
Circumpolaire sterren op het Noordelijk halfrond
****************************************************************
Circumpolair is de aanduiding die gebruikt wordt voor een hemellichaam dat (voor waarnemers op een bepaalde breedtegraad) nooit onder de horizon verdwijnt. Voor een noorderbreedte van 52º geldt bijvoorbeeld dat alle sterren met een declinatie van meer dan +38º circumpolair zijn. De bekendste circumpolaire sterrenbeelden zijn Ursa Major (Grote Beer of big dipper), Ursa Minor (Kleine Beer of little dipper), Cepheus en Cassiopeia. Voor een waarnemer op een van de polen van de aarde zijn alle (zichtbare) sterren circumpolair; voor een waarnemer op de evenaar is geen enkele ster circumpolair.
Bestudeer eerst bovenstaande cursus.
IN ONDERSTAANDE GEGEVENS STAAN ER VAAK HYPERLINKS. KLIK ER OP EN LEES OOK DIE TEKSTEN.
ER WORDEN DAAR VRAGEN OVER GESTELD.
Antwoorden te halen uit bovenstaande gegevens. Selecteer het antwoord dat je het meest juist lijkt en/of vul in.
MEN KAN DE OEFENING OOK OPNIEUW MAKEN, DOOR MET DE RECHTERMUISTOETS OP HET SCHERM TE KLIKKEN EN DAN IN HET GEOPENDE VENSTER, INDIEN HET WOORD ER STAAT, TE KLIKKEN OP "VERNIEUWEN"
Hoeken
 Hoeken kunnen worden gemeten in verschillende eenheden. Meestal uit men ze in graden. Net zoals een uur kan worden onderverdeeld in 60 minuten en een minuut van de tijd kan worden verdeeld in 60 seconden, kan een graad worden verdeeld in 60 boogminuten en een boogminuut kan verdeeld worden in 60 boogseconden.
Hoeken kunnen worden gemeten in verschillende eenheden. Meestal uit men ze in graden. Net zoals een uur kan worden onderverdeeld in 60 minuten en een minuut van de tijd kan worden verdeeld in 60 seconden, kan een graad worden verdeeld in 60 boogminuten en een boogminuut kan verdeeld worden in 60 boogseconden.1 ° = 1 graad = 60' = 60 boogminuten
1' = 60" = 60 boogseconden
1 ° = 3600"
Extra uitleg over het begrip decimale graad. Klik hier.
Extra uitleg over het begrip ruimtehoek. Klik hier.
Werken met radialen: 2 pi radialen = 360 ° en 1 radiaal = 57,3 °.
Extra uitleg over het begrip radiaal. Klik hier.
Extra uitleg over het begrip sterradiaal. Klik hier.
Hoeken kan men op verschillende manieren benoemen. Bijvoorbeeld, in deze driehoek
 De hoek a kan ook worden opgeroepen BAC, en de hoek b kan ook worden opgeroepen ABC.
De hoek a kan ook worden opgeroepen BAC, en de hoek b kan ook worden opgeroepen ABC.  Er zijn 90 ° in een rechte hoek.
Er zijn 90 ° in een rechte hoek.De 3 hoeken van een driehoek zijn samen 180° groot: a + b + c = 180 °.

Er zijn 360 ° in een cirkel.


Hoeken en lijnen
 Wanneer twee lijnen elkaar snijden worden 4 hoeken gecreëerd. Elke twee overstaande hoeken zijn gelijk en de twee hoeken die naast elkaar liggen bedragen samen 180 °.
Wanneer twee lijnen elkaar snijden worden 4 hoeken gecreëerd. Elke twee overstaande hoeken zijn gelijk en de twee hoeken die naast elkaar liggen bedragen samen 180 °.  Wanneer twee lijnen evenwijdig zijn (zoals AB en CD), en gesneden worden door een lijn (EF) dan zijn de overliggende hoeken gelijk. ook de verwisselende binnehoeken en verwisselende buitenhoeken zijn 2 aan 2 gelijk. In combinatie met de bovenstaande regel, ziet men dat alle 4 de hoeken, gemarkeerd in het rood, gelijk zijn.
Wanneer twee lijnen evenwijdig zijn (zoals AB en CD), en gesneden worden door een lijn (EF) dan zijn de overliggende hoeken gelijk. ook de verwisselende binnehoeken en verwisselende buitenhoeken zijn 2 aan 2 gelijk. In combinatie met de bovenstaande regel, ziet men dat alle 4 de hoeken, gemarkeerd in het rood, gelijk zijn. Cirkels
 d = 2 r (diameter = 2 maal de straal)
d = 2 r (diameter = 2 maal de straal) c = pi d = 2 p r (de omtrek = pi maal de diameter of pi maal 2 keer de straal).
oppervlakte is pi r2 (de oppervlakte = straal maal straal maal pi) (pi = 3,14159 ... ).
De kleine hoek formule
Omtrek cirkel (c) = 2 pi r. De afstand van een deel van de cirkelomtrek berekenen. Bv. van de boog gemarkeerd door de letter s.

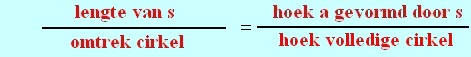
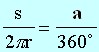
Waarom is deze formule zo goed? Omdat ze kan gebruikt worden voor dingen die geen deel uitmaken van een cirkel, zolang de hoek klein is! Bijvoorbeeld, wanneer de hoek klein is (minder dan 25), de driehoek hieronder heeft een zeer kleine scherpe hoek a en s is uiterst klein. Voor deze driehoek, is het een goede benadering om te zeggen dat s, r, gerelateerd zijn aan de kleine hoek formule. Nu heeft men inderdaad een zeer krachtig instrument , omdat men veel van de astronomie problemen kan omzetten in foto's met zeer kleine driehoeken.
Hoekmaten
In de sterrenkunde bestudeert men het heelal vanop de aarde. Dit betekent dat men de grootte van objecten niet kan meten met behulp van een liniaal. Dus vanuit de aardse observatie, berekent men vaak de grootte van een object met behulp van een te meten hoek. Als men geluk heeft iets over de afstand van een object te weten, dan kan men met behulp van de kleine hoek formule een relatie leggen tussen de hoekgrootte en de lineaire maat . Dit is een zeer frequente manier van meten van objecten in de astronomie.
Stel dat men de hoogte van een toren die men van op een afstand van 200 m bekijkt moet bepalen. Men kijkt naar de hoogte van de toren onder een hoek van 10°. Zie onderstaande tekening en berekening.

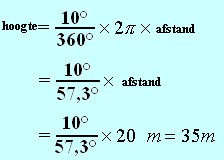
 De bovenste tekening toont aan dat twee objecten met verschillende grootte dezelfde hoekgrootte kunnen hebben indien zij worden bekeken vanaf verschillende afstanden. De hoekgrootte van het object wordt bepaald door de verhouding grootte / afstand. De lineaire grootte van het 2de object (2,5 cm) is 1,4 keer zo groot als het 1ste object (1,8 cm) en moet zodanig worden geplaatst dat het 1,4 keer verder staat om het onder dezelfde hoek te zien. Verplaatst men het 2de object twee maal dichter (zie onderste tekening) dan wordt de hoekgrootte tweemaal zo groot (20 graden ipv 10 graden).
De bovenste tekening toont aan dat twee objecten met verschillende grootte dezelfde hoekgrootte kunnen hebben indien zij worden bekeken vanaf verschillende afstanden. De hoekgrootte van het object wordt bepaald door de verhouding grootte / afstand. De lineaire grootte van het 2de object (2,5 cm) is 1,4 keer zo groot als het 1ste object (1,8 cm) en moet zodanig worden geplaatst dat het 1,4 keer verder staat om het onder dezelfde hoek te zien. Verplaatst men het 2de object twee maal dichter (zie onderste tekening) dan wordt de hoekgrootte tweemaal zo groot (20 graden ipv 10 graden).  In de praktijk kan men de hoekgrootte van voorwerpen (bomen, sterrenbeelden, vrienden) meten met behulp van diverse lichaamsdelen. In nevenstaande figuur is de hoekgrootte van de vuist bij getrekte arm ongeveer 10 graden en de pink ongeveer 1 graad.
In de praktijk kan men de hoekgrootte van voorwerpen (bomen, sterrenbeelden, vrienden) meten met behulp van diverse lichaamsdelen. In nevenstaande figuur is de hoekgrootte van de vuist bij getrekte arm ongeveer 10 graden en de pink ongeveer 1 graad. Samenvatting

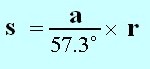
Merk op dat men de hoek in graden moet uitdrukken om de berekenigen naar behoren te verwerken. In de sterrenkunde werkt men met zeer kleine hoeken, gemeten in boogseconden. Men kan de graden veranderen in boogseconden met behulp van de conversie methoden.
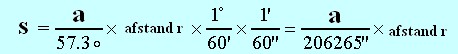
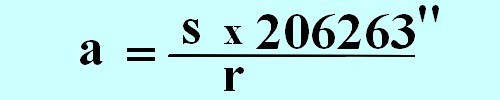
Voorbeeld van berekening:
Sommige objecten in de lucht hebben een schijnbare grootte - net als de maan. Door inzicht in de geometrie en de aard van een cirkel, is het mogelijk om de afstand te bepalen naar het object, of de fysieke diameter van het object. De standaard in de astronomie is de graad en de boogseconde. Hier zijn de conversie factoren:

Voor de bepaling van de fysieke diameter van Jupiter (op 26 juli 2003), kan men gebruik maken van de kleine hoek formule:
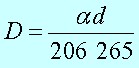 D = lineaire (fysieke) diameter.
D = lineaire (fysieke) diameter. α = hoekgrootte in boogseconden = bekend voor Jupiter 31,2 boogseconden.
d = de afstand tot object = bekend voor Jupiter = 943.000.000 km
206265 = boogseconden per radiaal.
 Dit is in goede overeenstemming met de werkelijke diameter van Jupiter (142.984 km).
Dit is in goede overeenstemming met de werkelijke diameter van Jupiter (142.984 km). Voor de berekening houdt men rekening met de straalbreking of refractie door de atmosfeer. Door de afbuiging van het licht kan men lichtstralen die hun oorsprong op 34 boogminuten (') onder de horizon hebben, al op de horizon waarnemen. Als het middelpunt van de zonneschijf, die zelf een diameter van ongeveer 32' heeft, nog 50' onder de horizon staat, ziet men de bovenrand al aan de horizon.
Als gevolg daarvan, duurt de dag rond 21 maart en rond 23 september, het begin van resp. lente en herfst, niet juist 12 uur, maar iets langer: 12 uur en 15 minuten. De duur van de schemering is 's avonds het tijdsinterval tussen zonsondergang en het ogenblik waarop de zon een aantal graden onder de horizon staat. 's Morgens is de schemering het interval tussen het ogenblik waarop de zon een aantal graden onder de horizon staat en de zonsopkomst.
Rechts boven: (achter days of year) tik je de datum in en kies je de maand of je verplaatst met de computermuis de rode pijl.
Observer's Latitude = breetegraad van de observeerder. Twee plaatsen met hun breedtegraad zijn reeds gegeven (Lincoln in Nebraska en Caïro in Egypte) Andere plaatsen kun je zelf kiezen. Achter latitude (breedte) tik je de gewenste breedtgraad in en kies je °N (noorderbreedte) of °S (zuiderbreedte) of je verplaatst met de computermuis de horizontale rode lijn op de wereldkaart.
Star Position = positie van de ster. Twee sterren met hun hemelcoördinaten zijn reeds gegeven (Sirius en Vega). Andere sterren kun je zelf kiezen door achter declination (declinatie) het gewenste getal in te tikken. Achter right ascension (rechte klimming) tik je ook het gewenste getal in. Zo heb je de hemelcoördinaten van de ster.
Klik je het keuzebolletje ("don't lock = niet vergrendelen) dan kun je met de computermuis de rode pijl over de tijdlijn bewegen. Over de wereldbol zie je dan de zon en de ster bewegen. Je kan ook de (sunrise) zonsopgang, de (noon) middagzon en de (sunset) zonsondergang aanklikken. Tenslotte kun je ook de (star rise) opkomst van de ster en de (star set) ondergang van de ster aanklikken. Een zwarte pijl duidt opkomst en ondergang van de ster aan op de tijdlijn. De blauwe lijn boven de tijdlijn geeft de tijd weer dat de ster (star above horizon) zichtbaar is boven de horizon. ook het (the start of twilight) beging van de schemering en het (the end of twilight) einde van de schemering kan men aanklikken.
Bestudeer eerst bovenstaande cursus.
IN ONDERSTAANDE GEGEVENS STAAN ER VAAK HYPERLINKS. KLIK ER OP EN LEES OOK DIE TEKSTEN.
ER WORDEN DAAR VRAGEN OVER GESTELD.
Antwoorden te halen uit bovenstaande gegevens. Selecteer het antwoord dat je het meest juist lijkt en/of vul in.
MEN KAN DE OEFENING OOK OPNIEUW MAKEN, DOOR MET DE RECHTERMUISTOETS OP HET SCHERM TE KLIKKEN EN DAN IN HET GEOPENDE VENSTER, INDIEN HET WOORD ER STAAT, TE KLIKKEN OP "VERNIEUWEN"
IN ONDERSTAANDE GEGEVENS STAAN ER VAAK HYPERLINKS. KLIK ER OP EN LEES OOK DIE TEKSTEN.
ER WORDEN DAAR VRAGEN OVER GESTELD.
Antwoorden te halen uit bovenstaande gegevens. Selecteer het antwoord dat je het meest juist lijkt en/of vul in.
MEN KAN DE OEFENING OOK OPNIEUW MAKEN, DOOR MET DE RECHTERMUISTOETS OP HET SCHERM TE KLIKKEN EN DAN IN HET GEOPENDE VENSTER, INDIEN HET WOORD ER STAAT, TE KLIKKEN OP "VERNIEUWEN"