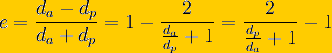ASTRONOMIE (begrippen)
***************************
Meten van afstanden
***************************
Afstand tot de maan
De afstand tot de maan is tot op een millimeter nauwkeurig gemeten door de looptijd van een laser (licht)bundel. De bemanning van Apollo 11 en ook latere bezoekers van de maan hebben er retroreflectors neergezet, dit zijn kubushoeken die licht terugkaatsen in de richting van waaruit het komt. Gemiddelde afstand tot de aarde 384.400 km
Afstanden binnen ons zonnestelsel
Afstanden in ons zonnestelsel zijn te meten uit de looptijd van licht van manen, bijvoorbeeld van Jupiter. Een andere methode is om precies de omlooptijd te meten en dan de afstand uit de wetten van Kepler te halen. De afstand tot Venus is tot op de kilometer gemeten door er een radarbundel op te laten weerkaatsen en de looptijd te meten.
Hoe ver is Venus van de Aarde verwijderd?
Venus is voor ons de meest nabije planeet maar de precieze afstand hangt af van de banen van de beide planeten. Beide planeten draaien in een ellipsvormige baan om de Zon dus de afstand tot Venus varieert steeds. Op het verste punt is Venus 261 miljoen kilometer van de Aarde verwijderd. Venus heeft 224,7 dagen nodig voor één omloop om de Zon. Iedere 584 dagen staan Venus en de Aarde het dichtste bij elkaar. Dan bedraagt de afstand gemiddeld 40 miljoen kilometer maar er zijn een paar uitzonderingen waarbij deze afstand tot 38 miljoen kilometer terug kan lopen.
Nabije afstanden binnen ons melkwegstelsel
Afstanden tot 7800 lichtjaar (pulsar PSR B1508+55) zijn te meten met de parallaxmethode. De ster wordt dan vanuit twee verschillende posities waargenomen. Die twee posities zijn twee punten in de baan van de aarde, dus met zes maanden tussentijd. Op telescoopfoto's wordt dan vergeleken over welke hoek in boogseconden de plaats van de ster afwijkt ten opzichte van de vaste sterren die veel verder staan. Een boogseconde of parsec bedraagt 3,26 lichtjaar. Zo staat de dichtstbijzijnde ster Proxima Centauri op 4 lichtjaar.
Een ster heeft ook een eigenbeweging. Er zijn dan ook minstens drie waarnemingen nodig, steeds met een half jaar tussenruimte. Uit het verschil tussen de eerste en de derde waarneming (die idealiter op dezelfde dag van het jaar gemaakt zijn) blijkt de eigenbeweging, uit het verschil met de tweede waarneming de afstand.
De astrometrische waarnemingen van de satelliet Hipparcos hebben 100.000 afstanden in onze melkweg nauwkeurig bepaald en 2,5 miljoen afstanden minder nauwkeurig.
Verre afstanden binnen ons melkwegstelsel en afstanden tot nabije melkwegstelsels
Afstanden tot 10.000 lichtjaar zijn te bepalen door vergelijking van de spectra van het licht dat sterren uitzenden. Als twee sterren eenzelfde spectrum hebben, dan zullen ze ook eenzelfde helderheid hebben. Vergelijking van de aangenomen intrinsieke helderheid (absolute magnitude) met de waargenomen schijnbare helderheid (schijbare magnitude) geeft een schatting van de afstand.
Relatie tussen de afstand en schijnbare en absolute helderheid van een ster. Klik hier.
Afstanden tot spiraalvormige sterrenstelsels
Voor nog grotere afstanden tot een spiraalvormig sterrenstelsel worden waarnemingen gedaan aan een specifiek type veranderlijke sterren, de zogenaamde Cepheïden. Hun helderheid verandert met een bepaalde periode. Uit de waarnemingen op kortere afstanden is gebleken dat Cepheïden met gelijke periode even helder zijn. Ongeveer 3 % van de sterren zijn Cepheïden. Het volstaat dus om van één Cepheïde in een sterrenstelsel de periode en de schijnbare helderheid te meten om de afstand tot het stelsel te kennen.
Afstanden tot elliptische sterrenstelsels
Voor nog grotere afstanden tot sterrenstelsels, in het bijzonder elliptische sterrenstelsels, worden superreuzen waargenomen. De Cepheïden zijn dan te zwak om nog waar te nemen, maar de superreuzen zijn de helderste stabiele sterren in het heelal. In een elliptisch sterrenstelsel komen geen Cepheïden voor. De veronderstelling is, dat alle sterren van het type superreus ongeveer dezelfde intrinsieke helderheid hebben. Uit de schijnbare helderheid volgt de afstand.
Afstanden tot quasars
Voor de grootste afstanden, bijvoorbeeld tot quasars tot 13,6 miljard lichtjaar, is roodverschuiving een algemeen toegepaste methode. In het spectrum van waterstof wordt een bepaalde spectraallijn waargenomen. Uit de meting hoever die spectraallijn naar het rood is opgeschoven, volgt met het Dopplereffect de theoretische snelheid van het sterrenstelsel. Uit afstandsmetingen op kortere afstanden is gebleken dat sterrenstelsels van elkaar wegvluchten, en wel met een grotere snelheid naarmate de afstand groter is (zie Oerknal en Wet van Hubble). Uit de gemeten snelheid volgt dus met de Hubbleconstante de afstand.
***********************
Afstandsmodulus
***********************
De afstandsmodulus is een manier binnen de astronomie om afstanden uit te drukken tot sterrenstelsels. De afstandsmodulus μ = m − M is het verschil tussen de schijnbare magnitude m en de absolute magnitude M van een astronomisch object. m − M = 5logd − 5
Weten we dan de afstandsmodulus μ = m − M, dan is de afstand in parsecs gegeven door: d = 100.2(m − M + 5) = 100.2μ + 1
Afstandsmoduli worden het meest gebruikt als de afstand tot een melkwegstelsel dat relatief dichtbij staat, moet worden uitgedrukt. Bijvoorbeeld, de Grote Magelhaense Wolk heeft een afstandsmodulus van 18,5, de Andromedanevel heeft een afstandsmodulus van 24,4 en de Virgocluster heeft een afstandsmodulus van 31,0. In het geval van de Grote Maghelaanse Wolk betekent dit dat de supernova SN1987A, met een maximale schijnbare magnitude van 2,8, een absolute magnitude had van -15,7 - vrij laag voor een supernova.
De magnitude van een ster
Is een getal dat de helderheid van een ster aangeeft. Men dient onderscheid te maken tussen de schijnbare helderheid van een ster en de absolute helderheid. De absolute helderheid van een ster, die direct samenhangt met de lichtkracht, is de helderheid die een ster zou hebben als deze op een afstand van 10 parsec (is gelijk aan 32,6 lichtjaar) stond. Zo heeft de zeer heldere ster Sirius (8,7 lichtjaren) een schijnbare magnitude van -1,46 en een absolute magnitude van (+) 1,43 (op een bijna 4 maal zo grote afstand zou hij bijna 16 maal zo zwak zijn, wat de magnitude bijna 3 hoger zou maken). Onze zon zou een absolute magnitude van + 4,88 hebben en daarmee een onopvallende maar nog wel met het blote oog zichtbare ster zijn. Er wordt ook onderscheid gemaakt tussen visuele- en fotografische magnitude, sterren hebben verschillende kleuren (zie ook spectraalklasse) en het blote oog heeft zijn maximale gevoeligheid in het geel, terwijl fotografische platen meer gevoelig zijn voor blauw en violet. Een blauwe ster zal in verhouding dus helderder lijken op een fotografische plaat. Voor objecten binnen ons zonnestelsel, zoals planetoïden is de absolute helderheid gedefinieerd als de helderheid wanneer het object op precies één A.E. van de zon zou staan.
Zichtbaarheid
Afhankelijk van de omstandigheden kunnen sterren tot een bepaalde magnitude met het blote oog gezien worden. In een stad met veel lichtvervuiling zullen misschien sterren tot een grensmagnitude 2 gezien kunnen worden, op een hoge bergtop ver van alle omgevingslicht is de grensmagnitude ongeveer 6. Dit is geen absolute grens, het hangt ook van de waarnemer zelf af en zelfs van de manier van kijken. De gele vlek in het centrum van het gezichtsveld is minder gevoelig voor licht dan de gebieden met staafjes er naast, maximale gevoeligheid wordt bereikt door net "naast" het object te kijken. Dit noemt men ook wel "perifeer waarnemen". Met een telescoop worden sterren met hogere magnitudes (dus zwakkere) zichtbaar. Hoeveel zwakker hangt af van de verhouding in oppervlakte van (de pupil van) het blote oog en die van het objectief van de telescoop. Een pupil heeft in het donker een diameter van ongeveer 6 mm, een (relatief kleine) telescoop van 60 mm levert dan al een factor 100 op, en dus een winst van 5 magnituden. De grensmagnitude zal hier dus 11 zijn. Grotere telescopen leveren meer winst op, voor iedere factor 10 in diameter dus 5 magnitudes.
De schijnbare helderheid of magnitude van sterren
Werd in de oudheid reeds aangegeven met getallen: de helderste sterren kende men de magnitude of grootte 1 toe en de zwakste de magnitude 6. Een klein getal betekent dus een grote helderheid. Te onderscheiden zijn de schijnbare helderheid (zoals wij deze waarnemen) en de absolute helderheid ofwel de helderheid die een ster zou hebben als ze op een afstand van 10 parsec stond. Later heeft men deze helderheidsschaal uitgebreid en verfijnd, waarbij afgesproken is dat een verschil in magnitude van 5 overeenkomt met een helderheidsverhouding van een factor 100. De magnitude is dus een logaritmische schaal waarbij een verschil in magnitude van 1 overeenkomt met een helderheidsverhouding van 2,512. Enkele hemellichamen zijn zo helder dat hun magnitude negatief is. De zon heeft op een onbewolkte dag een magnitude van -26,5, wat men ook noteert als -26m,5 of -26,5 mag, de volle maan heeft op een heldere nacht een magnitude van -12,5.
De absolute helderheid of magnitude van sterren
Is een maat voor de werkelijke lichtkracht ervan. De absolute helderheid is de helderheid die een hemellichaam zou hebben als het zich op de overeengekomen afstand van exact 10 parsec zou bevinden. Ze wordt uitgedrukt in magnitudes. De absolute helderheid van een object hangt alleen af van de werkelijke lichtkracht (omdat alle objecten daarvoor op een gelijke afstand worden 'gezet'). De schijnbare helderheid (zoals we die waarnemen) hangt ook af van de afstand tussen de waarnemer en het object. Als m de schijnbare helderheid van het object is en r de afstand, uitgedrukt in parsec, dan wordt de absolute helderheid gegeven door M = m + 5 - 5*log(r). Een ster van absolute helderheid 0 is 82,4 keer helderder dan de Zon. De helderste sterren zijn van absolute helderheid -7 of -8, de zwakste zitten boven magnitude 15. Voor een planetoïde of komeet is de absolute helderheid de werkelijke helderheid die het object zou hebben op een afstand van 1 Astronomische Eenheid van zowel de Aarde als de Zon.
************************************************
De parallax als maat voor de afstand
************************************************
De Aarde beweegt in een nagenoeg perfecte cirkelbaan omheen de Zon. Als we vanop Aarde een vaste ster waarnemen op verschillende tijdstippen van het jaar, en we gaan ervan uit dat we zelf stilstaan, dan schijnt de ster een cirkel van precies dezelfde afmeting te beschrijven in de ruimte. Door het perspectief-effect kan deze cirkel afgeplat worden tot een ellips (des te platter naarmater de ster dicht bij de ecliptica ligt). De lange as van de ellips is echter steeds twee astronomische eenheden (AE) groot. Eén AE bedraagt 150 miljoen kilometer.
We noemen de parallax van de ster: de helft van de schijnbare lengte van die lange as, uitgedrukt in boogseconden. Er bestaat een rechtstreeks verband tussen de parallax van een ster en haar afstand tot het zonnestelsel: hoe verder de ster verwijderd is, hoe kleiner haar parallax; en hoe dichterbij de ster, hoe groter haar parallax.
Dit verband kunnen we zelfs mathematisch uitdrukken door de driehoek te analyseren gevormd door enerzijds de ster, anderzijds de Aarde in twee tegenoverliggende posities op haar baan om de Zon.
Parallaxen zijn erg kleine hoeken. Bij dergelijke kleine hoeken kan men met zeer grote nauwkeurigheid de sinus van een hoek vervangen door de hoek zelf, op voorwaarde dat de hoek uitgedrukt wordt in radialen:
p (in rad) = R/d
Willen we de parallax toch in boogseconden blijven uitdrukken, dan volstaat het de omrekeningsfactor van radialen naar boogseconden (180 x 3600 / Pi = 206264,8...) in rekening te brengen.
p (") = 206264,8 R/d
De afstand R tussen de aarde en de Zon bedraagt precies 1, op voorwaarde dat we hem uitdrukken in astronomische eenheden (AE). 1 AE bedraagt ongeveer 150 miljoen km. Maar dan wordt ook de afstand d tussen de aarde en de ster uitgedrukt in AE. Deze eenheid wordt in de interstellaire ruimte al gauw onpraktisch, want te klein. Daarom voeren we voor het gemak een nieuwe lengtemaat in, de parsec, (parallax-seconde, afkorting pc), die ongeveer gelijk is aan 206265 AE.
We krijgen dan de eenvoudige formule
p (") = 1/d (pc)
of omgekeerd, indien de sterparallax rechtstreeks gemeten wordt,
d = 1/p
De parsec of pc is de meest gebruikte afstandsmaat bij beroepsastronomen. Veelvouden zijn de kiloparsec (kpc), Megaparsec (Mpc) en Gigaparsec (Gpc).
************************
Wetten van Kepler
************************
De wetten van Kepler zijn een drietal natuurkundige wetten op het gebied van de mechanica, opgesteld door Johannes Kepler, die de bewegingen van de planeten beschrijven.
Eerste wet
De eerste wet van Kepler zegt dat alle planeten zich rond de zon bewegen in elliptische banen, waarbij de zon zich in één van de brandpunten van de ellips bevindt. De som van de afstanden van de planeet naar beide brandpunten is overal op de ellips gelijk.
Tweede wet
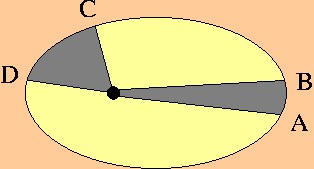
De perkenwet: als een planeet in dezelfde tijd van A naar B en van C naar D gaat, zijn de gearceerde oppervlakten even groot.
De snelheid van een planeet in haar omloopbaan verandert zodanig dat in gelijke tijdsintervallen de oppervlakte, bestreken door de rechte lijn (voerstraal) tussen de zon en de planeet, gelijk is. De voerstraal beschrijft dus in gelijke tijdsintervallen, gelijke oppervlakken, ook perken genoemd, vandaar de naam perkenwet. In het getoonde voorbeeld is de gemiddelde snelheid van de planeet in het interval AB dus kleiner dan in het interval CD. Dit toont eveneens aan dat de grootte van de omloopsnelheid van een planeet niet constant is.
De perkenwet is een meetkundige formulering van het behoud van draaimoment. Als v de snelheidsvector van de planeet voorstelt, en s de positievector van de planeet ten opzichte van de zon, dan is het draaimoment evenredig met het kruisproduct s * v . Het gekleurde segment in de figuur is de integraal van de grootte van s * v over een gegeven tijdsinterval.
Deze behoudswet is geldig bij elke centrale kracht en hangt niet af van de bijzondere vorm van de zwaartekracht. Als de planeten door middel van elastiekjes met de zon verbonden waren, dan gold de perkenwet nog steeds! (maar de banen zouden geen ellipsen zijn)
Derde wet
Het kwadraat van de omlooptijd (t) van een planeet is evenredig met de derde macht van haar gemiddelde afstand (r) tot de zon ofwel:
t2 / r3 = constant
Deze wet wordt ook wel de harmonische wet genoemd. Isaac Newton voegde later een term toe die afhangt van de massa van de planeet: alleen als de planeet veel lichter is dan de ster waarom hij draait geldt de derde wet van Kepler als speciaal geval. Deze wet werd door Kepler pas tien jaar na zijn andere twee wetten gepubliceerd. Meer bepaald geldt dat:
t2 / r3 = (4π2) / G * M
waarin M de massa van de ster is en G de universele gravitatieconstante.
Indien de massa van de planeet niet verwaarloosbaar is wordt wel eens (M+m) ingevuld in de formule in plaats van M, hierin is m dan de massa van de planeet.
De wet is als volgt te herleiden:
Fc = Fg
(met Fc = middelpuntzoekende kracht en Fg = gravitatiekracht),dus:
(m * v2) / r = (G * m * M) / r2
(waarin v de snelheid van de desbetreffende planeet is.)
v2 / r = (G * M) / r2
dus: v2 = (G * M) / r
dus: v2 / r = G * M
dus: ((2π * r) / t)2) * r = G * M (substitueer: v = (2π * r) / t)
dus: ((4π2 * r2) / t2) * r = G * M
dus: r3 / t2 = (G * M) / 4π2
Vergelijking van Kepler
Uit de eerste twee wetten leidde Kepler ook een praktische bewegingsvergelijking af, die in de hemelmechanica bekend staat als de vergelijking van Kepler. Deze vergelijking verklaart de niet-uniforme beweging van de planeet op haar baan in termen van een wiskundige hulpgrootheid, de excentrische anomalie.
Hoe ver is Venus van de Aarde verwijderd?
Venus is voor ons de meest nabije planeet maar de precieze afstand hangt af van de banen van de beide planeten. Beide planeten draaien in een ellipsvormige baan om de Zon dus de afstand tot Venus varieert steeds. Op het verste punt is Venus 261 miljoen kilometer van de Aarde verwijderd. Venus heeft 224,7 dagen nodig voor één omloop om de Zon. Iedere 584 dagen staan Venus en de Aarde het dichtste bij elkaar. Dan bedraagt de afstand gemiddeld 40 miljoen kilometer maar er zijn een paar uitzonderingen waarbij deze afstand tot 38 miljoen kilometer terug kan lopen.
Een ster heeft ook een eigenbeweging. Er zijn dan ook minstens drie waarnemingen nodig, steeds met een half jaar tussenruimte. Uit het verschil tussen de eerste en de derde waarneming (die idealiter op dezelfde dag van het jaar gemaakt zijn) blijkt de eigenbeweging, uit het verschil met de tweede waarneming de afstand.
De astrometrische waarnemingen van de satelliet Hipparcos hebben 100.000 afstanden in onze melkweg nauwkeurig bepaald en 2,5 miljoen afstanden minder nauwkeurig.
Weten we dan de afstandsmodulus μ = m − M, dan is de afstand in parsecs gegeven door: d = 100.2(m − M + 5) = 100.2μ + 1
Afstandsmoduli worden het meest gebruikt als de afstand tot een melkwegstelsel dat relatief dichtbij staat, moet worden uitgedrukt. Bijvoorbeeld, de Grote Magelhaense Wolk heeft een afstandsmodulus van 18,5, de Andromedanevel heeft een afstandsmodulus van 24,4 en de Virgocluster heeft een afstandsmodulus van 31,0. In het geval van de Grote Maghelaanse Wolk betekent dit dat de supernova SN1987A, met een maximale schijnbare magnitude van 2,8, een absolute magnitude had van -15,7 - vrij laag voor een supernova.
Zichtbaarheid
Afhankelijk van de omstandigheden kunnen sterren tot een bepaalde magnitude met het blote oog gezien worden. In een stad met veel lichtvervuiling zullen misschien sterren tot een grensmagnitude 2 gezien kunnen worden, op een hoge bergtop ver van alle omgevingslicht is de grensmagnitude ongeveer 6. Dit is geen absolute grens, het hangt ook van de waarnemer zelf af en zelfs van de manier van kijken. De gele vlek in het centrum van het gezichtsveld is minder gevoelig voor licht dan de gebieden met staafjes er naast, maximale gevoeligheid wordt bereikt door net "naast" het object te kijken. Dit noemt men ook wel "perifeer waarnemen". Met een telescoop worden sterren met hogere magnitudes (dus zwakkere) zichtbaar. Hoeveel zwakker hangt af van de verhouding in oppervlakte van (de pupil van) het blote oog en die van het objectief van de telescoop. Een pupil heeft in het donker een diameter van ongeveer 6 mm, een (relatief kleine) telescoop van 60 mm levert dan al een factor 100 op, en dus een winst van 5 magnituden. De grensmagnitude zal hier dus 11 zijn. Grotere telescopen leveren meer winst op, voor iedere factor 10 in diameter dus 5 magnitudes.
We noemen de parallax van de ster: de helft van de schijnbare lengte van die lange as, uitgedrukt in boogseconden. Er bestaat een rechtstreeks verband tussen de parallax van een ster en haar afstand tot het zonnestelsel: hoe verder de ster verwijderd is, hoe kleiner haar parallax; en hoe dichterbij de ster, hoe groter haar parallax. Dit verband kunnen we zelfs mathematisch uitdrukken door de driehoek te analyseren gevormd door enerzijds de ster, anderzijds de Aarde in twee tegenoverliggende posities op haar baan om de Zon.
Parallaxen zijn erg kleine hoeken. Bij dergelijke kleine hoeken kan men met zeer grote nauwkeurigheid de sinus van een hoek vervangen door de hoek zelf, op voorwaarde dat de hoek uitgedrukt wordt in radialen:
p (in rad) = R/d
Willen we de parallax toch in boogseconden blijven uitdrukken, dan volstaat het de omrekeningsfactor van radialen naar boogseconden (180 x 3600 / Pi = 206264,8...) in rekening te brengen.
p (") = 206264,8 R/d
De afstand R tussen de aarde en de Zon bedraagt precies 1, op voorwaarde dat we hem uitdrukken in astronomische eenheden (AE). 1 AE bedraagt ongeveer 150 miljoen km. Maar dan wordt ook de afstand d tussen de aarde en de ster uitgedrukt in AE. Deze eenheid wordt in de interstellaire ruimte al gauw onpraktisch, want te klein. Daarom voeren we voor het gemak een nieuwe lengtemaat in, de parsec, (parallax-seconde, afkorting pc), die ongeveer gelijk is aan 206265 AE.
We krijgen dan de eenvoudige formule
p (") = 1/d (pc)
of omgekeerd, indien de sterparallax rechtstreeks gemeten wordt,
d = 1/p
De parsec of pc is de meest gebruikte afstandsmaat bij beroepsastronomen. Veelvouden zijn de kiloparsec (kpc), Megaparsec (Mpc) en Gigaparsec (Gpc).
Eerste wet
De eerste wet van Kepler zegt dat alle planeten zich rond de zon bewegen in elliptische banen, waarbij de zon zich in één van de brandpunten van de ellips bevindt. De som van de afstanden van de planeet naar beide brandpunten is overal op de ellips gelijk.
Tweede wet
De perkenwet: als een planeet in dezelfde tijd van A naar B en van C naar D gaat, zijn de gearceerde oppervlakten even groot.
De snelheid van een planeet in haar omloopbaan verandert zodanig dat in gelijke tijdsintervallen de oppervlakte, bestreken door de rechte lijn (voerstraal) tussen de zon en de planeet, gelijk is. De voerstraal beschrijft dus in gelijke tijdsintervallen, gelijke oppervlakken, ook perken genoemd, vandaar de naam perkenwet. In het getoonde voorbeeld is de gemiddelde snelheid van de planeet in het interval AB dus kleiner dan in het interval CD. Dit toont eveneens aan dat de grootte van de omloopsnelheid van een planeet niet constant is.
De perkenwet is een meetkundige formulering van het behoud van draaimoment. Als v de snelheidsvector van de planeet voorstelt, en s de positievector van de planeet ten opzichte van de zon, dan is het draaimoment evenredig met het kruisproduct s * v . Het gekleurde segment in de figuur is de integraal van de grootte van s * v over een gegeven tijdsinterval.
Deze behoudswet is geldig bij elke centrale kracht en hangt niet af van de bijzondere vorm van de zwaartekracht. Als de planeten door middel van elastiekjes met de zon verbonden waren, dan gold de perkenwet nog steeds! (maar de banen zouden geen ellipsen zijn)
Derde wet
Het kwadraat van de omlooptijd (t) van een planeet is evenredig met de derde macht van haar gemiddelde afstand (r) tot de zon ofwel:
t2 / r3 = constant
Deze wet wordt ook wel de harmonische wet genoemd. Isaac Newton voegde later een term toe die afhangt van de massa van de planeet: alleen als de planeet veel lichter is dan de ster waarom hij draait geldt de derde wet van Kepler als speciaal geval. Deze wet werd door Kepler pas tien jaar na zijn andere twee wetten gepubliceerd. Meer bepaald geldt dat:
t2 / r3 = (4π2) / G * M
waarin M de massa van de ster is en G de universele gravitatieconstante.
Indien de massa van de planeet niet verwaarloosbaar is wordt wel eens (M+m) ingevuld in de formule in plaats van M, hierin is m dan de massa van de planeet.
De wet is als volgt te herleiden:
Fc = Fg
(met Fc = middelpuntzoekende kracht en Fg = gravitatiekracht),dus:
(m * v2) / r = (G * m * M) / r2
(waarin v de snelheid van de desbetreffende planeet is.)
v2 / r = (G * M) / r2
dus: v2 = (G * M) / r
dus: v2 / r = G * M
dus: ((2π * r) / t)2) * r = G * M (substitueer: v = (2π * r) / t)
dus: ((4π2 * r2) / t2) * r = G * M
dus: r3 / t2 = (G * M) / 4π2
Vergelijking van Kepler
Uit de eerste twee wetten leidde Kepler ook een praktische bewegingsvergelijking af, die in de hemelmechanica bekend staat als de vergelijking van Kepler. Deze vergelijking verklaart de niet-uniforme beweging van de planeet op haar baan in termen van een wiskundige hulpgrootheid, de excentrische anomalie.
